السلام عليكم
هميلتون هو فيزيائى وفلكى ورياضى وقام باسهامات عديدة فى مجال الفيزياء ورياضيات ويرجع له الفضل فى وضع كل من مبدأ الفعل الاقل فى الميكانيكا
و الهملتونيان وهى دالة فى احداثيات عامة وتمثل الطاقة الكلية المحفوظة لاى منظومة فيزيائية
و مسار هملتون
وزمرة هملتون فى نظرية المجموعات (رياضيات)
فضاء هملتون الاتجاهى (رياضيات)
ومعادلة هملتون-جاكوب والتى تستخدم فى الفيزياء وفى حساب الاسطح الريمانية فى الرياضيات
الكواتيرنيون Quaternions رياضيات
البايكوتيرنيون Biquaternions الرياضيات
الفرسر versor وهو عبارة عن جزء من دائرة عظمى ذات اتجاه (اى دائرة على سطح ريمانى مركزها هو مركز السطح تسمى دائرة عظمى مثل دوائر الطول والعرض فى الكرة الارضية) تقابل الكوترنيون
والعديد من المبادئ الفيزيائية والرياضية
معادلة هملتون-جاكوب هى معادلة تفاضلية جزيئية غير خطية من الدرجة الاولى فى متغير يسمى بدالة هملتون الاساسية وهى عبارة عن دالة مولدة generating function اما من الناحية الفيزيائية فهى ترتبط بدالة الفعل الكلاسيكية ومعادلة هملتون جاكوب تستخدم لايجاد التغير الزمنى للاحداثيات المعممة generalized coordinates وتستخدم فى حساب التغاير calculus of variations وفى حساب الجيودسك فى الاسطح الريمانية فى الهندسة التفاضلية وايضا فى هندسة الربط symplectic geometry فى الهندسة الجبرية
اما عن ربط بين قوانين الميكانيكا التقليدية و قوانين البصريات:
فهو لايرجع الى معادلة هملتون-جاكوب وانما يرجع الى مبدأ الفعل الاقل اما معادلة هملتون-جاكوب فهى تحقق هذا التكافؤ بين الميكانيكا التقليدية وبين علم البصريات وفكرة الربط هى مثلما ان الضوء يسلك اقصر مسار ويتحرك فى اقل زمن فان مبدأ هملتون ينص ان المنظومة الحركية تتحرك بحيث يكون لها اقل فعل (الفعل هو التكامل الزمنى لدالة لاجرانج وهى بدورها تحويل لجتدر للهملتونيان)
و لماذا قيل أن معادلته لها شكل موجي ؟
لا ادرى ....
وعلى العموم فان معادلة الموجة هى معادلة من الدرجة الثانية اما معادلة هملتون-جاكوب فهى معادلة من الدرجة الاولى
=0)
ولا ادرى ان كان هناك ربط ام لا. اما اذا تنازلنا عن قوانين النسبية الخاصة (معاملة المكان والزمان بنفس الطريقة ) اى عند سرعات منخفضة فانه يكون لدينا معادلة من الدرجة الثانية فى الاحداثيات المكانية ومن الدرجة الاولى فى الزمن فنحصل على معادلة تشبة معادلة الموجة .
اذا اعتمدنا التغير من الدرجة الاولى فى الزمن:
اذا بدلنا علاقة التبادلية فى ميكانيكا الكم بقوسى بويسون واخذنا النهاية عند ثابت بلانك يساوى الصفر وسرعة الضوء تساوى مالانهاية فى معادلة الموجة فى نظرية المجال الكمى نحصل على معادلة هملتون جاكوب
عند اخذ سرعة الضوء تساوى مالانهاية تؤول قوانين ميكانيكا الكم النسبوية QFT الى قوانين ميكانيكا الكم QM
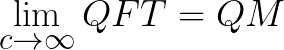
اى تؤول معادلة الموجة الى معادلة هايزنبيرج للحركة فى ميكانيكا الكم (وهى المعادلة المقابلة لمعادلة شرودنجر فى ميكانيكا الموجية)
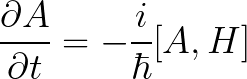
وهى تقابل معادلات هملتون للحركة عند تبديل علاقة التبادلية باقواس بوايسون
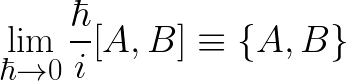
حيث تعرف اقواس بوايسون بالمعادلة التالية
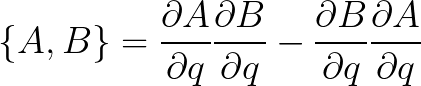
وعند تعويض B=H الهملتونيان واستخدام المعادلات القانونية Canonical equations نحصل على معادلة هملتون جاكوب
اذا اعتمدنا التغير من الدرجة الثانية فى المكان
بنفس المنطلق نجد ان معادلة الموجة تؤول الى معادلة شرودنجر عند سرعات منخفضة وهى ايضا تؤول بدورها الى معادلة هملتون جاكوب عند اخذ نهاية ثابت بلانك تساوى الصفر
وهكذا لا ادرى ان كانت معادلة هملتون جاكوب لها شكل موجة بشكل عام ... ولكن فقط تحت بعض الشروط التى ذكرناها سابقا فان معادلة الموجة تؤول الى معادلة هملتون-جاكوب
والله اعلم