يمكن بسهولة التأكد من أن 1! و 2! و 3! و 4! لا تصلح وأن 5!+5 مكعب كامل

فإذا كان

مكعباً كاملاً يقبل القسمة على الخمسة فإنه يقبل القسمة على 125 أيضاً
حيث أن المكعبات الكاملة التي تقبل القسمة على 5 يمكن كتابتها

ولكن هذا غير صحيح لأنه لكل

فإن

فمثلا
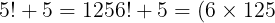-5(6+1)\\%20%207!+5=(7\times6\times125)-5((7\times6)+1))
وهكذا ... هناك حد لا يقبل القسمة على 125
أو بصورة أخرى لكل m>15 :

ويمكن التأكد من المضاريب الباقية بسهولة
سنجد أن m!+5 لكل m>5 لا يقبل القسمة على 125
أي أنه لا يوجد m>5 يجعل m!+5 مكعبا كاملا
وبالتالي فإن هناك حل وحيد وهو m=5