
25-08-2010, 20:36
|

|
|
تاريخ التسجيل: Jan 2008
الدولة: السعودية - جدة
المشاركات: 1,584
|
|
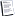 رد: " المسابقة الرياضية الكبرى "
رد: " المسابقة الرياضية الكبرى "

المشاركة الأصلية كتبت بواسطة Weierstrass-Casorati
يمكن بسهولة التأكد من أن 1! و 2! و 3! و 4! لا تصلح وأن 5!+5 مكعب كامل

فإذا كان  مكعباً كاملاً يقبل القسمة على الخمسة فإنه يقبل القسمة على 125 أيضاً
حيث أن المكعبات الكاملة التي تقبل القسمة على 5 يمكن كتابتها

ولكن هذا غير صحيح لأنه لكل  فإن 
فمثلا
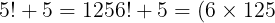-5(6+1)\\%20%207!+5=(7\times6\times125)-5((7\times6)+1))
وهكذا ... هناك حد لا يقبل القسمة على 125
أو بصورة أخرى لكل m>15 :

ويمكن التأكد من المضاريب الباقية بسهولة
سنجد أن m!+5 لكل m>5 لا يقبل القسمة على 125
أي أنه لا يوجد m>5 يجعل m!+5 مكعبا كاملا
وبالتالي فإن هناك حل وحيد وهو m=5 |
الحقيقة البرهان أحسه غير مقنع ...
اضافة الى الخطوة
 ولكن هذا غير صحيح لأنه لكل
ولكن هذا غير صحيح لأنه لكل  فإن فإن 
|
تحتاج لبرهان ...
لفكرة أسهل فكر باستخدام التطابقات ، واختر اساس مناسب للتطابق ، راح تصل وبسهولة ...
|