ملتقى الفيزيائيين العرب - عرض مشاركة واحدة

زولديك · #6 16-09-2010, 23:03

القيمة العددية التي يتساوىعندها الدليل السفلي و العلوي( $n-2\Rightarrow (n-2)2\Rightarrow (n/2)-1\Rightarrow n-((n/2)-1)=(n/2)+1$ ) و هدا الحد هو الحد المنصف للحدود كلها في حالة ان عدد الحدود عدد زوجي و و لا وجود له في حالة انه عدد فردي
عدد الحدود هو

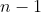
( $n-1$ ) و سنستفيد من هده المعلومة عند كالتالي

( $log_n(1/2)=-1log_n(2)$ )
نستنتج ان

( $log_n(2).log_{n-1}3.......log_{(n/2)+1}((n/2)+1).log_{n/2}((n/2)+2).log_{(n/2)-1}((n/2)+3)......log_{2}(n).(-1)^{n-1}$ ) و الآن باخد الحدود إبتداءا من الحد الاول و هو

( $log_{n}2$ )إلى الحد الدي يسبق الحد المنصف و هو ( $log_{(n/2)+2}(n/2)$ ) انصل للتعبير التالي

( $log_{n}2.log_{n-1}3....log_{(n/2)+2}(n/2)$ ) , الآن ناخد جميع الحدود إبتداءا من الحد الاخير و هو

( $log_{2}(n)$ ) إلى الحد الدي يسبق الحد المنصف و هو

( $log_{n/2}((n/2)+2)$ ) و هكدا نحصل على التعبير التالي

( $log_{2}(n).log_{3}(n-1).......log_{n/2}((n/2)+2)$ ) , الآن نكتب التعبيرين السابقين معا لنجد التعبير التالي

( $log_{n}(2).log_{n-1}3..........log_{(n/2)+1}((n/2)+1).......log_{3}(n-1).log_{2}(n) (-1)^{n-1}=log_{n}(2).log_{n-1}3..........log_{(n/2)+1}((n/2)+1).log_{3}(n-1).log_{2}(n).(-1)^{n-1}$ ) , اي ان كل حد له ضده , و لكي نثيت ان عدد الحدود متساوي على يمين المنصف و يساره , لاحظ ان المنصف هو

( $(n/2)+1$ ) و بجمع عليه عدد الحدود المتبقى و هو

( $(n/2)-1$ )لنستنتج ان الحد الآخير هو

( $((n/2)+1)+((n/2)-1)=n$ ) و هو الحد الآخير من متتابعة ما داخل اللوغاريتم , كدلك بانسبة للديل السفلي و نطرح من عدد الحدود المتبقى لنجد ان

( $((n/2)+1)-((n/2)-1)=2$ ) هو قيمة الحد الآخير من متتابعة الاساس و و هكدا نستنتج ان قيمة حاصل الضرب هو

(-1) في حالة أن (n-1) هو عدد فردي , بينما يكون حاصل الضرب هو (+1) إدا كان (n-1) هو عدد زوجي . انتأكد مما قلت و لنأخد مسالة الحد المنصف و انا قلت أن الحد المنصف هو

( $(n/2)+1$ ) أي انه إدا كانت n=4 فإن قيمة الحد المنصف هو

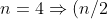( $n=4\Rightarrow (n/2)+1 \Rightarrow (4/2)+1=3$ ) اي عند هده القيمة يتساوى الدليل السفلي و العلوي ,ايضا لاحظ ان قيمة حاصل الضرب حسب ما قدمت يكون (-1) لنتأكد من دلك

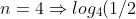( $n=4\Rightarrow log_{4}(1/2).log_{3}(1/3).log_{2}(1/4)=log_{4}2.log_{3}3.log_{2}4(-1).(-1).(-1)=-1$ ) ايضا لنأخد n=5 في هده الحالة لا وجود للمنصف إد لا معنى له و يكون قيمة حاصل الضرب هو الواحد (+1) , لنتاكد من دلك

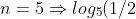( $n=5\Rightarrow log_{5}(1/2).log_{4}(1/3).log_{3}(1/4).log_{2}(5)=(-1).(-1).(-1).(-1).log_{5}(2).log_{4}(3).log_{3}(4).log_{2}(5)=+1$ )
مرة اخرى لنأخد n=6 اي ان المنصف هو (4) بمعنى هده هي القيمة التي يتساوى عندها ما بداخل اللوغاريتم مع اساسه , و قيمة حاصل الضرب هي (-1) لأن 6-1=5 , و هو فردي , لنتأكد من دلك

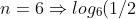( $n=6\Rightarrow log_{6}(1/2).log_{5}(1/3).log_{4}(1/4).log_{3}(5).log_{2}(6)=(-1)(-1).(-1).(-1).(-1).log_{6}(2).log_{5}(3).log_{4}(4).log_{3}(5).log_{2}(6)=-1$ ) أخيرا كما قال الإمام الشافعي راي صواب يحتمل الخطأ و رأي غيري خطأ يحتمل الصواب , فأرجو من اخيتي "نورة الشريف "ان تصوبني إلى خطأي مع جزيل الشكر .