ملتقى الفيزيائيين العرب - عرض مشاركة واحدة

الصادق · #5 24-11-2010, 17:19

المشاركة الأصلية كتبت بواسطة زولديك

لتكن لدينا المتسلسلة
${\color{blue} \sum_{1}^{n \to \infty }[x^{\frac{1}{n}}-1]=(x-1)+(\sqrt{x}-1)+(\sqrt{\sqrt{x}}-1)+....}$

الآن كحالة خاصة و ذلك عندما x=1 نستنج ان المتسلسلة تؤول إلى الصيغة
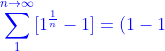${\color{blue} \sum_{1}^{n \to \infty }[1^{\frac{1}{n}}-1]=(1-1)+(\sqrt{1}-1)+(\sqrt{\sqrt{1}}-1)+....}=0$ أي أن المتسلسلة لها مجموع , و ذلك يعني ان المتسلسلة تقاربية عندما x=1 و لكن كون المتسلسلة تقاربية ذلك يعني بالضرورة كون المتتابعة الخاصة بالمتسلسلة تؤول إلى الصفر أي ان

${\color{blue} \sum_{1}^{n \to \infty }[1^{\frac{1}{n}}-1]=0\Rightarrow \lim_{n \to \infty }[1^{\frac{1}{n}}-1=0]}$ و من هذا الأخير نستنج ان

${\color{blue}\Rightarrow \lim_{n \to \infty }1^{\frac{1}{n}}-1=0\Rightarrow \lim_{n \to \infty }1^{\frac{1}{n}}=1\therefore 1^{0}=1}$ و سبب توقفي عند

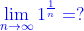${\color{blue} \lim_{n \to \infty }1^{\frac{1}{n}}=?}$ هو عدم معرفتي لقيمة هذه النهاية , و لكنها "أي قيمة النهاية"أصبحت معادلة بمجهول واحد و من ثم نتجت قيمتها

اظنك تقصد
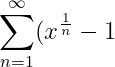$\150dpi \sum_{n=1}^{\infty}(x^\frac{1}{n}-1)=(1-1)+(\sqrt{1}-1)+(1^{\frac{1}{3}}-1)+\cdots+(1^{\frac{1}{n}}-1)+\cdots$
ولكن انت تريد ان تبرهن ان 1 مرفوع للقوة صفر يساوي 1 وهنا انت استخدمت ما تريد برهانه في خطوات الحل
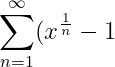$\150dpi \sum_{n=1}^{\infty}(x^\frac{1}{n}-1)=(1-1)+(\sqrt{1}-1)+(1^{\frac{1}{3}}-1)+\cdots+(1^{\frac{1}{n}}-1)+\cdots\stackrel{?}{=}0$
ايضاً لاحظ ما الذي يمنع من الاجراء التالي :
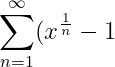$\150dpi \sum_{n=1}^{\infty}(x^\frac{1}{n}-1)=1-(1-\sqrt{1})-(1-1^{\frac{1}{3}})-\cdots-(1-1^{\frac{1}{n}})-\cdots\stackrel{?}{=}1$
اي دمج الحد الثاني مع الثالث والرابع مع الخامس ...الخ

هذا والله تعالى اعلم