
24-11-2010, 17:34
|

|
|
تاريخ التسجيل: Feb 2008
الدولة: سوريا
المشاركات: 1,342
|
|
 رد: برهان تحليلي
رد: برهان تحليلي
[IMG][/IMG]

المشاركة الأصلية كتبت بواسطة الصادق
اظنك تقصد
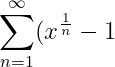=(1-1)+(\sqrt{1}-1)+(1^{\frac{1}{3}}-1)+\cdots+(1^{\frac{1}{n}}-1)+\cdots)
ولكن انت تريد ان تبرهن ان 1 مرفوع للقوة صفر يساوي 1 وهنا انت استخدمت ما تريد برهانه في خطوات الحل
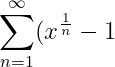=(1-1)+(\sqrt{1}-1)+(1^{\frac{1}{3}}-1)+\cdots+(1^{\frac{1}{n}}-1)+\cdots\stackrel{?}{=}0)
ايضاً لاحظ ما الذي يمنع من الاجراء التالي :
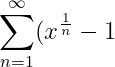=1-(1-\sqrt{1})-(1-1^{\frac{1}{3}})-\cdots-(1-1^{\frac{1}{n}})-\cdots\stackrel{?}{=}1)
اي دمج الحد الثاني مع الثالث والرابع مع الخامس ...الخ
هذا والله تعالى اعلم |
لم أفهم اعتراضك اخي الكريم نحن لدينا المتسلسلة
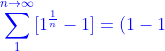+(1^{\frac{1}{2}}-1)+(1^{\frac{1}{3}}-1)+...}) و نستطيع غختصار الحدود و ذلك بحساب الجذر التربيعي للواحد و من ثم الجذر التكعيبي للواحد و من ثم الجذر الرابع للواحد و من ثم الجذر المليون للواحد و هكذا دواليك و في كل مرة يكون الناتج في ما بين القوسين هو الصفر أي ان مجموع حدود المتسلسلة هو الصفر و من هنا نستنتج التقارب فها تقول لي كف اعتمدت على ما اريد برهانه في البرهان؟:emot30_astonishe: و نستطيع غختصار الحدود و ذلك بحساب الجذر التربيعي للواحد و من ثم الجذر التكعيبي للواحد و من ثم الجذر الرابع للواحد و من ثم الجذر المليون للواحد و هكذا دواليك و في كل مرة يكون الناتج في ما بين القوسين هو الصفر أي ان مجموع حدود المتسلسلة هو الصفر و من هنا نستنتج التقارب فها تقول لي كف اعتمدت على ما اريد برهانه في البرهان؟:emot30_astonishe:
|