أهلا وسهلا بك إلى ملتقى الفيزيائيين العرب.
أهلا وسهلا بك زائرنا الكريم، إذا كانت هذه زيارتك الأولى للمنتدى، فيرجى التكرم بزيارة صفحة التعليمـــات، بالضغط هنا.
كما يشرفنا أن تقوم بالتسجيل بالضغط هنا إذا رغبت بالمشاركة في المنتدى، أما إذا رغبت بقراءة المواضيع والإطلاع فتفضل بزيارة القسم الذي ترغب أدناه.
| ملتقى الفيزيائيين العرب > قسم المنتديات العامة > منتدى الفيزياء العام | ||
| أعظم معادلة في الفيزياء. | ||
| الملاحظات |
|
|
أدوات الموضوع | انواع عرض الموضوع |
|
#1
|
|||
|
|||
|
أترككم مع الصورة:
 |
|
#2
|
|||
|
|||
|
إنزين عندي سؤال
المعادلة لا تساوي الصفر؟ على العموم مشكور على الموضوع |
|
#3
|
|||
|
|||
|
للأسف نعم المعادلة =صفر حتى أنا كنت شاك فيها لكن المعادلة لا تسمى بهذا الاسم الا اذا كان طرفيها متساويين
|
|
#4
|
|||
|
|||
|
مشكور اخوي لكن هذه المعادله خاص باي جزء من الفيزيا
|
|
#5
|
|||
|
|||
|
طيب برجع من جديد للموضوع الصورة م طالعة مؤقتا عندي شكرا لك
|
| متفيزقة مبدعة |
| مشاهدة ملفه الشخصي |
| البحث عن كل مشاركات متفيزقة مبدعة |
|
#6
|
|||
|
|||
|
هذي هي الصورة بعد مشقة عدت وحملتها
 طيب معادلة حلوة انا حليتها بالمرة الاولى صفر كطلع والمرة الثانيه لا لكن برجع للرموز وبشوف شكرا لك |
| متفيزقة مبدعة |
| مشاهدة ملفه الشخصي |
| البحث عن كل مشاركات متفيزقة مبدعة |
|
#7
|
|||
|
|||
|
السلام عليكم ورحمة الله وبركاته اخي مهند
بعد عناء في ايجاد الصورة انا ماطلع عندي لكن iهو عدد مركب كونه كذا هو عطاك قيمته -1لأنه مركب على هالأساس انا اعتقد انو نقدر نوصل لها لما نجيب من القيمة الافتراضية له في معادلة التربيع للعدد السالب في ح س^2+1=0 لما ننقل الواحد يصير سالب واحد وعلى كذا نجيب الجذر التربيعي للطرفين اووكي فيستحيل حلها في ح ونحلها في كـ وهذي المجموعة يكون عندها -1ه قيمة ت وهو العدد الخيالي او الافتراضي وجود قيمته -1 من هالمعادلة اللي متبتها اعتقد نقدر نوصل لمعادله اللي موجودة من خلال كذا لكن انا تفاجأت طلعت اول مرة وفي الثانيه ماطلعت مدري شنو سويت نسيت بس اعتقد هالمعادله فيها شئ ا لكن اتمنى انك تقول لنا لو تعرف شئ اكثر عنها نبغى نعرف اذا مو مشكلة اووكي انتظر ردك وشرحك لهذي المعادلة موفق بإذن الله ... لك مني أجمل تحية . |
| متفيزقة مبدعة |
| مشاهدة ملفه الشخصي |
| البحث عن كل مشاركات متفيزقة مبدعة |
|
#8
|
|||
|
|||
|
إنزين ما إطلعت معاي حتى لما حاولت إشوي بمحاولات متقدمة بالآلة الحاسبه
log e(-1) ≠ iπ بجرب أحاول مره ثانية |
|
#9
|
|||
|
|||
|
يا جماعة.. دي أجمل معادلة في الرياضيات مش في الفيزياء.. مالهاش دلالات فيزيائية إلا في التطبيق
ولقبت بأجمل معادلة رياضية لأن فيها أهم خمس أرقام في الرياضيات، بالإضافة إلى وجود أهم تلات عمليات رياضية مرة واحدة فقط (الجمع والضرب والرفع لأس) وإثباتها بسيط جدًا من صيغة أويلر، ضع المتغير يساوي باي.   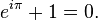 للمزيد من المعلومات: http://en.wikipedia.org/wiki/Euler%27s_identity |
|
#10
|
|||
|
|||
|
هذه تحوي عدد تخيلي.
x +yi=re^ia a تساوي باي r^2=x^2+y^2 r=x cos"a" iy=r sin"a" e^iπ=-1 r=1 x=-1 y=0 e^iπ=-1+0=-1 e^iπ+1=0 |
«
الموضوع السابق
|
الموضوع التالي
»
| الذين يشاهدون محتوى الموضوع الآن : 1 ( الأعضاء 0 والزوار 1) | |
| انواع عرض الموضوع |
 العرض العادي العرض العادي |
 الانتقال إلى العرض المتطور الانتقال إلى العرض المتطور |
 الانتقال إلى العرض الشجري الانتقال إلى العرض الشجري |
|
|
المواضيع والمشاركات المنشورة لا تعبر عن رأي ملتقى الفيزيائيين العرب ولانتحمل أي مسؤولية قانونية حيال ذلك ويتحمل كاتبها مسؤولية النشر"
الساعة الآن 11:09



