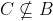ملتقى الفيزيائيين العرب - عرض مشاركة واحدة

تغريـد · #1 17-03-2010, 22:22

[OVERLINE]المجموعات الجزئية[/OVERLINE]

تعريف : يقال لمجموعة B أنها مجموعة جزئية من مجموعة A
إذا كان كل عنصر ينتمي للمجموعة B فإنه ينتمي أبضا إلى ِA
و نرمز لذلك ب
$B \subset A$

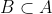ملاحظة: 1-من الواضح أنه حسب التعريف السابق فإن إي مجموعة هي مجموعة جزئية من نفسها .
2- إذا كانت B مجموعة جزئية من A و لكنها لا تساويها نقول أن Bمجموعة جزئية فعلية من A

ملاحظة:
أـ هناك بعض الكتب تستخدم التعبير
$B \subset A$
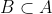
لتعني أن كل عناصر B محتواه في A بغض النظر عن إمكانية A=B (إمكانية محتملة)
وعندما تريد أن تقول أن B مجموع جزئية من A و في نفس الوقت تنفي التساوي فإنها ترمز لذلك ب
$B \varsubsetneq A$

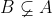
بـ بينما هناك كتب أخرى تستخدم الصيغة
$B \subset A$
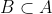
لتعني هنا أن B محتواه في A و لكنها لا تساويها

و تستخدم الصيغة
$B \subseteq A$
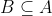
لتشمل إمكانية التساوي

مثال: إذا كانت A هي مجموعة الاعداد الزوجية
$A=\{2n: n \in Z\}$
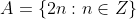
و كانت B مجموعة الأعداد الطبيعية الزوجية
$B=\{2n: n \in N \}$

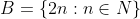
و كانت C مجموعة الأرقام الزوجية
$C= \{0,2,4,6,8,10\}$
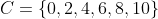
فإن
$B \subset A$

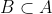
و كذلك
$C \subset A$

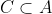
و لكن المجوعة C ليست مجموعة جزئية من B. لماذا؟

و نرمز لذلك ب
$C \nsubseteq B$